RF power measurements rely on test equipment, such as peak power sensors, average power sensors,...
What Is Power & Why Is It Essential for RF & Microwave Systems?
Wireless systems rely on measuring RF and microwave power accurately and efficiently. Noise can mask signals that are too low in power, which decreases the signal-to-noise ratio (SNR) and increases the bit error rate (BER). Signals that exceed acceptable levels can cause distortion and saturation.
In the post below, learn the fundamentals of power and how to best characterize the power of AC waveforms.
What Is Power?
A common explanation for power derives from physics, where power is defined as the transfer rate of energy per unit time.

Energy has many forms, including mechanical, electrical, chemical, thermal, radiant, and nuclear. All these forms fall under two broad categories – potential energy and kinetic energy. Imagine a tree with a large red apple dangling from one of its branches. Right now, the apple has potential energy, or energy that is stored due to its position. If the apple were to suddenly fall from the tree and hit the ground, the potential energy would convert to kinetic energy, which is the energy of an object in motion.
Mechanical Power
One way to describe mechanical energy is an object's ability to do "work" based on its motion (kinetic) or position (potential). In physics, work is defined as the amount of energy transferred when a force causes an object to move or displace by some distance. Work is measured in joules (J) and is calculated by Work = Force x Distance.
To calculate mechanical power, we need to know the rate or amount of time it took to complete the work done (transfer of energy) on an object (Power Mechanical = Force x Distance / Time). Since the distance an object traveled divided by the time is equal to velocity, mechanical power can also be expressed as multiplying force and velocity (Power Mechanical = Force x Velocity).
Say someone needs to push a couch across a room. If the couch is pushed from point A to point B very slowly, the person uses minimal power and needs a lot of time to complete the task. If the couch is pushed from point A to point B quickly, the person exerts more power to accomplish the task in a shorter timeframe. In the two scenarios, the same amount of work is done but the power ratings differ.
Electrical Power
Electrical energy derives from the potential energy and kinetic energy of charged particles (e.g., electrons).
Recall that mechanical power is equal to force times velocity. The driving cause for the movement of electrons is known as voltage or the electromotive force (EMF). Just as water needs some sort of pressure to flow through a pipe, voltage causes electrons to move through a conductor. The SI unit for voltage is volts (V).
An electric current is the rate at which electrons move through a conductor over time, similar to velocity for mechanical power. In the water analogy, an electric current is likened to the rate that water flows through a pipe. The SI unit for current is ampere (A).
Using the information above, the equation for electrical power expressed in watts (W) is calculated by Power Electrical = EMF x Current.
Power Measurements & AC Waveforms
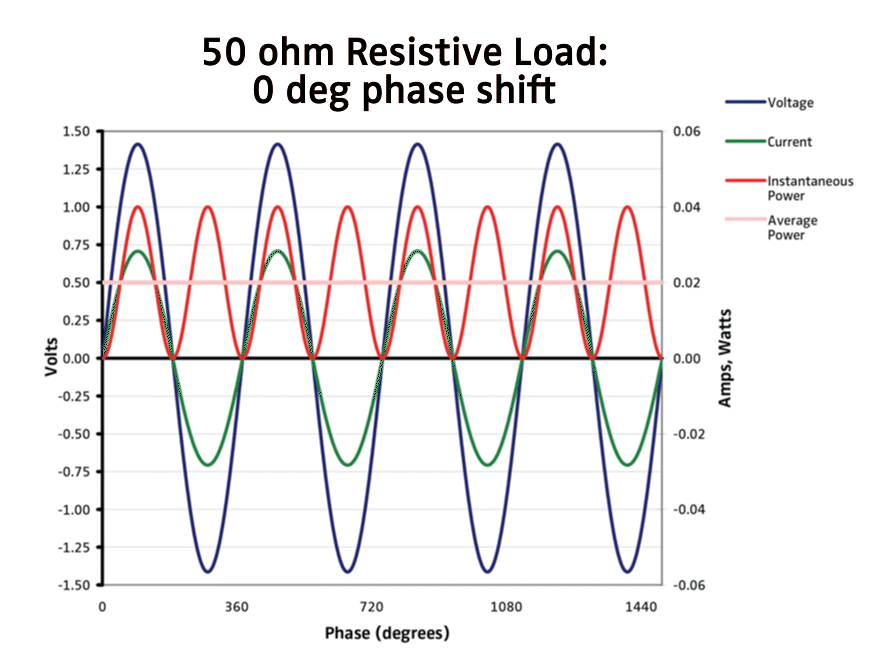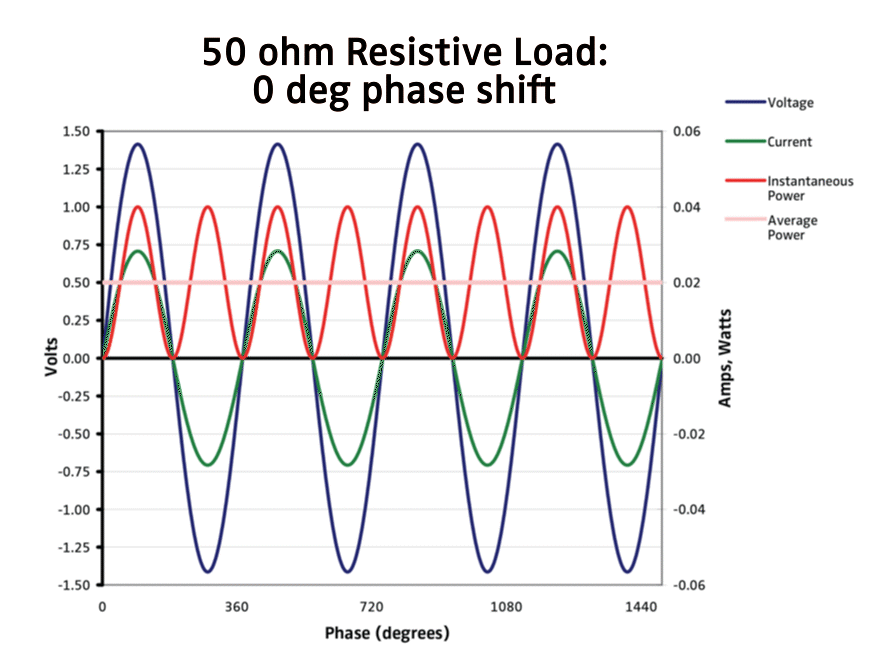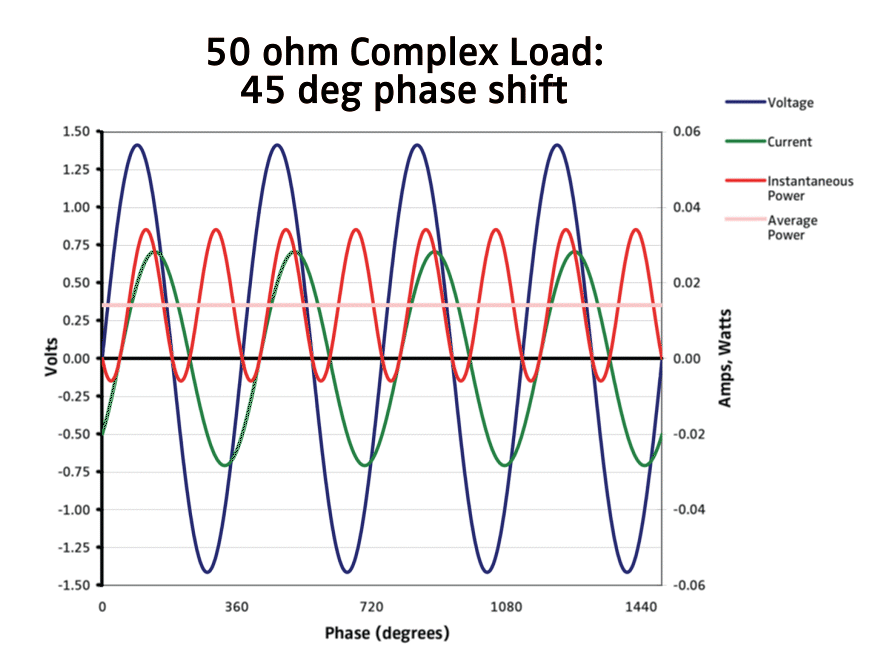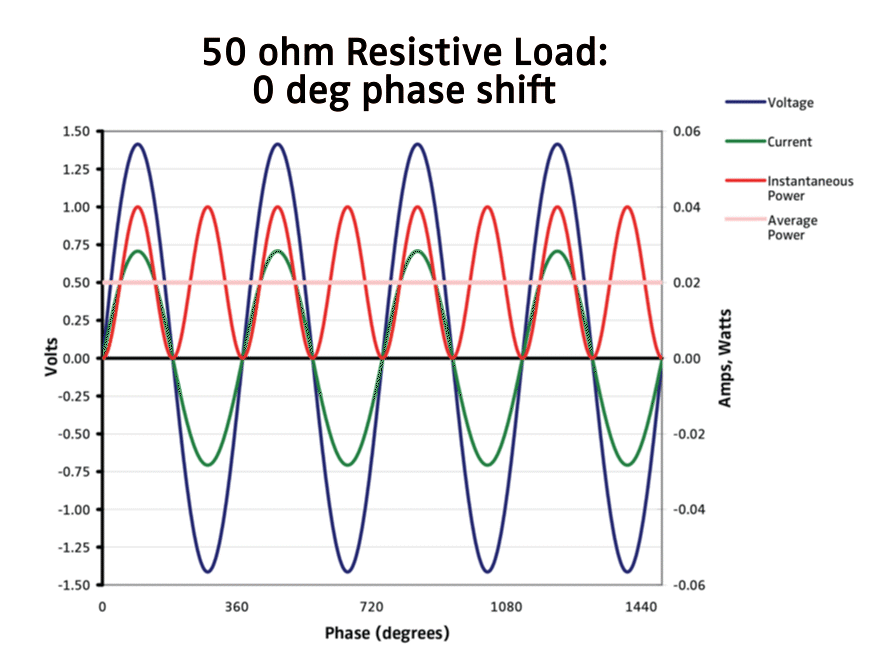
AC waveforms continuously change direction and magnitude with time. A common example of an AC waveform is a sine wave. As the current and voltage fluctuate, so does the instantaneous power.
Current and voltage are in-phase for resistive loads. Both reach positive peak values, cross the x-axis, and dip to negative peak values together over time. With matching polarities, Power Electrical = EMF x Current will always yield a positive result.
If there is a phase shift, moments arise where the polarities of voltage and current are out of sync, resulting in a negative power value that affects instantaneous and average power measurements. Average power is computed by averaging the instantaneous power over at least one single period.
Direct power measurements maintain a near in-phase voltage and current relationship by applying an RF signal to a load element, which ultimately avoids erroneous results.
How is RF power actually detected by test instruments? Uncover the answer in the Boonton power measurement poster, article series, and previous blog posts.



